Failures of the Z' definition

Error message

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in _menu_load_objects() (line 579 of /home3/kirsty/public_html/zprime/includes/menu.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters in drupal_get_feeds() (line 394 of /home3/kirsty/public_html/zprime/includes/common.inc).

When is Z' > 1 not Z' > 1 ?

Z' is strictly defined as the number of formula units in the unit cell divided by the number of independent general positions. In reality however, the situation is often much more complicated than this and in many cases the derived Z' value is either at best only of limited use or, at worst, can be deceptive and lead to the loss of important packing information.

Some common flaws/misconceptions are outlined below.

  • Definition of the "Formula Unit"
  • Z' = 0.5 + 0.5 = 1
  • Supramolecular vs Covalent Interactions
  • Crystallography vs Chemistry
  • References

Definition of the "Formula Unit"

The definition of the "formula unit", the smallest representative unit of a crystal structure is a subjective judgement. The formula unit may contain several kinds of molecules or indeed assemblies of molecules and therefore it is not always straightforward to assign. This problem is especially acute in ionic compounds where there may be several chemically different cations, anions and/or neutral molecules present in the structure. The situation is further muddled if there is a charge imbalance requiring a greater number of one ion over another, or if the nature of the counterions is not clear. The formula unit in solvates or co-crystals can also prove problematic to assign, particularly in non-stoichiometric compounds.

For example consider the hydrated mixed sulfate/hydrogen sulfate salt of diprotonated 1,2-phenylenediamine, formula unit [C6H4(NH3)22+]8·(SO4)6·(HSO4)4·8H2O (Z' = 8, Z" = 24).1 The formula is assigned in this way based on charge-balance considerations, however the protons could not be precisely located in the difference map and therefore their exact disposition is unclear as there could be a number of possible combinations of SO42-/HSO4-/H2SO4/H3O+ or H2O species present, e.g. the formula could equally be represented as: [C6H4(NH3)22+]8·(SO4)7·(HSO4)3·(H3O)·7H2O or [C6H4(NH3)22+]8·(SO4)8·(H2SO4)2·8H2O (although there must be at least six sulfate anions to ensure charge balance). Thus here the Z' value is difficult to assign as the formula unit is essentially indefinable without further experiments (such as single crystal neutron diffraction), it is therefore assigned as Z' = 8 due to the presence of eight 1,2-phenylenediammonium anions in the asymmetric unit.

 

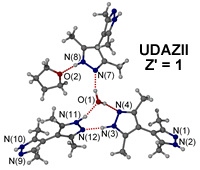
For neutral compounds there can also be confusion. The compound with CSD refcode UDAZII2 has the molecular formula 3(C10H14N4).THF.H2O (Z" = 5) and is described as a Z' = 1 structure as the "formula unit" contains three bipyrazolyl molecules together with one water and one THF molecule. However it could be argued that this would be better described as a Z' = 3 structure as the three bipyrazolyl molecules are in different environments in the crystal.

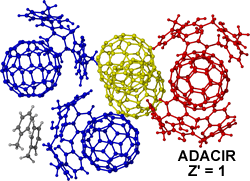Another example of packing complexity is in ADACIR,3 a calix[5]arene Buckminsterfullerene complex (calix[5]arene)4.(C60)5.(toluene)2 which has 11 unique molecules in the asymmetric unit (Z" = 11) but is correctly reported as Z' = 1 (according to the definition). The five C60 molecules are in three different environments within the crystal, one C60 is encapsulated by two calixarenes, two C60 molecules are each found in the cavity of one calixarene and there are two free in the lattice. The description of this complicated packing arrangement is unfortunately lost in the current Z' description.

Consider also Sodium 1,2-benzisothiazol-3(2H)-onate 1,1-dioxide hydrate (LANBOS)4 which has the formula (C7H4NSO3Na)16 (H2O)30, in the assignment of Z' (16) the water molecules have not been considered and it could be argued that this is a Z' = 2 structure with the formula unit being (C7H4NSO3Na)8 (H2O)15. Again this oversimplified definition fails to recognise the complexity of the packing and a Z' = 16 description is justified in this instance.

Z' = 0.5 + 0.5 = 1

Another example where packing information is lost are structures which crystallise with molecules on special positions, as this leads to the asymmetric unit containing fractions of molecules.

The asymmetric unit of N,N'-bis(phthaloyl)-(1R,2R)-1,2-diaminocyclohexane (GOXBUQ)5 for example contains two half molecules and is therefore described as Z' = 1 (as obviously 0.5 + 0.5 = 1) even though the situation with two symmetry unique (fragments of) molecules is conceptually identical to Z' = 2, albeit with added molecular symmetry.

 

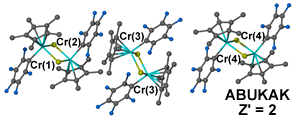
This issue becomes exponentially more complicated as Z' values increase, for example both bis((μ2-Chloro)-(perfluorophenyl)-(η5-pentamethylcyclopentadienyl)-chromium(iii)) (ABUKAK, 1 whole molecule plus two half molecules)6 and (2Z,8Z)-1,4,7,10-Tetrathiacyclododeca-2,8-diene (MUGZUJ, four half molecules)7 have to be described as Z' = 2 as the current definition is not flexible enough to include more complicated values.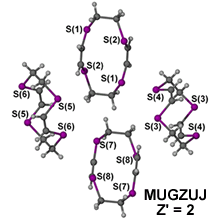

 

Supramolecular or Covalent interactions?

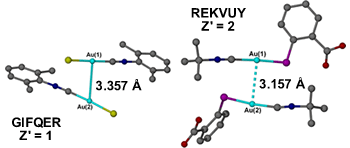When does a short intermolecular interaction become a formal covalent bond, or at least an intramolecular bond? What about cases where there are long-range weak covalent or dative bonds? There are some cases where the boundaries between a strong intermolecular interaction and a formal covalent bond are somewhat blurred, such as for gold···gold interactions. The asymmetric unit of dichloro-bis((o-xylylisocyano)-gold(i)) (GIFQER)8 for example contains two molecules linked by a gold···gold interaction of 3.357 Å which is assigned in the CSD as a formal single covalent bond and hence Z' = 1. t-Butylisonitrile-(thiosalicylic acid-S)-gold(i) (REKVUY)9 on the other hand has a similar arrangement of molecules again linked by a gold···gold interaction, this time shorter at 3.157 Å but this is assigned as a non-covalent interaction and hence Z' = 2.

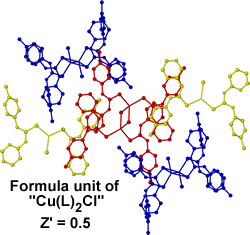Assigning Z' values in labile systems can also be a conceptual challenge. The labile copper(I)complex "CuCl(L)2" where L = (1-pyridin-2-yl-3-p-tolyl-thiourea)10crystallises in a remarkable arrangement with three chemically distinct isomeric forms present in the crystal; a [Cu(L)2Cl] monomer, an S-bridged dimer [{Cu(L)(μ-(L))Cl}2] and a Cl-bridged dimer [{Cu(L)2(μ-Cl)}2]. The asymmetric unit itself contains one monomer, one Cl-bridged dimer and an S-bridged dimer sitting on a crystallographic inversion centre, thus with the above formula unit Z' is assigned as 0.5. As the system is so labile there is, however, an argument for regarding the long Cu-S and Cu-Cl interactions in the dimers as intermolecular interactions rather than formal covalent bonds and hence defining the formula unit as "CuL2Cl" which would make the structure Z' = 4.

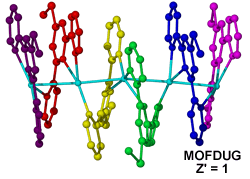Similar to the Cu(I) example above, [(Ag5L26)(BF4)5].4MeNO2 (where L2 = 4'-thiomethyl-2,2':6',2"-terpyridine, MOFDUG)11 is another example of an extended array formed by potentially labile bonds. Varying the solvent and counterions used in the system causes formation of a diverse array of structures containing the Ag(L2) subunit with assemblies ranging from polynuclear supramolecular spirals to aggregates of monomers.10 The large structural diversity is believed to be due to frustration between a number of competing labile metal to ligand, solvent and counterion interactions and the non-complementary shape of the ligand.

 

Crystallography vs Chemistry

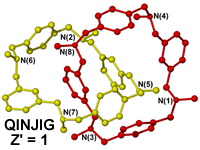
Classes of compounds such as catenanes and rotaxanes contain two (or more) interlocked molecules which cannot be chemically separated, i.e. cannot be split apart without breaking a covalent bond. In a crystallographic sense however, technically a catenane consists of two interlinked independent molecules and hence could be described as Z' = 2 structure. The current trend seems to be to assign catenanes as Z' = 1 (e.g. QINJIG)12 but again here important information regarding the exact nature of the molecule is lost.

It is clear from all the examples above that there are many pitfalls and issues to consider when assigning a value of Z' to a structure. If you would like to comment on any of the above or have encountered any other problems then please let us know.

References

  1. K. M. Anderson, A. E. Goeta, K. S. B. Hancock and J. W. Steed, Chem. Commun., 2006, 2138
  2. I. Boldog, E. B. Rusanov, A. N. Chernega, J. Sieler and K. V. Domasevitch, Angew. Chem., Int. Ed., 2001, 40, 3435
  3. J. L. Atwood, L. J. Barbour and C. L. Raston, Cryst. Growth Des., 2002, 2, 3
  4. (a) R. Banerjee, P. M. Bhatt, M. T. Kirchner and G. R. Desiraju, Angew. Chem., Int. Ed., 2005, 44, 2515 (b) P. Naumov, G. Jovanovski, O. Grupce, B. Kaitner, A. D. Rae, and S. W. Ng, Angew. Chem., Int. Ed., 2005, 44, 1251
  5. J. Gawronski, F. Kazmierczak, K. Gawronska, U. Rychlewska, B. Norden and A. Holmen, J. Am. Chem. Soc., 1998, 120, 12083
  6. M. Ganesan and F. P. Gabbai, Organometallics, 2004, 23, 4608
  7. T. H. Staeb, R. Gleiter and F. Rominger, Eur. J. Org. Chem., 2002, 2815
  8. H. Ecken, M. M. Olmstead, B. C. Noll, S. Attar, B. Schlyer and A. L. Balch, J. Chem. Soc., Dalton Trans., 1998, 3715
  9. W. Schneider, A. Bauer and H. Schmidbaur, Organometallics, 1996, 15, 5445
  10. J. T. Lenthall, K. M. Anderson, S. J. Smith and J. W. Steed, Cryst. Growth Des., manuscript in preparation
  11. M. J. Hannon, C. L. Painting, E. A. Plummer, L. J. Childs and N. W. Alcock, Chem. Eur. J., 2002, 8, 2226
  12. N. Watanabe, Y. Furusho, N. Kihara, T. Takata, K. Kinbara and K. Saigo, Chem. Lett., 1999, 915